Зміст
· Вступ
· Система підвіски
· Модель шин
∘ MF94
∘ MFTire 5.2
∘ Інші явища, що підлягають моделюванню
· Типові проблеми та рішення з MF
· Висновок
Вступ
Будучи студентом другого курсу спеціальності "Ігрове програмування" в BUAS і палким фанатом автомобілів та двигунів внутрішнього згоряння, я завжди знаходив тему симуляції транспортних засобів в реальному часі (для ігор) надзвичайно цікавою.
Для середнього розробника ігор симуляція транспортних засобів часто спрощується, оскільки робота та зусилля, необхідні для реалістичної симуляції, — це велика задача, і в кінцевому рахунку, не завжди є доцільною. Це через те, що 1: легкодоступні, зрозумілі ресурси в цій галузі є рідкісними. 2: можна обійтись нереалістичною поведінкою, але все одно зробити це виглядати і відчуватися переконливо, і 3: реалізація стабільної реалістичної поведінки динаміки транспортних засобів може бути надзвичайно часозатратною.
Якщо ви хочете досягти реалістичності, немає простого і швидкого способу зробити це. Ось чому в цій статті я хочу поділитися своїми знаннями щодо моделей шин і їх динаміки, щоб полегшити вам цей процес. Спочатку ми поговоримо про реалізацію деякої форми підвіски, оскільки вона потрібна для реалістичного перенесення ваги транспортного засобу, що, в свою чергу, необхідне для реалістичної симуляції шин.
Система підвіски
Щоб симульований транспортний засіб поводився реалістично, нам завжди потрібна якась система підвіски. Це виходить із поведінки транспортних засобів у реальному житті, оскільки підвіска необхідна для комфорту водія і для покращення характеристики проходження поворотів у екстремальних ситуаціях. Для нас вона служить ще однією метою — ми можемо легко отримати поточне навантаження на колесо, до якого вона підключена, що є важливим параметром для моделі шини.
Системи підвіски насправді є досить складними в реальному житті, оскільки це складання кількох механічних частин, таких як кульові опори, амортизатори, контролюючі важелі тощо. Тому реалістична симуляція підвіски — це величезне завдання саме по собі, і це не те, на чому ми будемо зосереджуватись у цій статті.
Натомість ми можемо обійтися підходом зі пружиною та амортизатором. Згідно з законом Гука, пружина з амортизатором виглядає так:
де F — сила в Н, k — коефіцієнт жорсткості, X — зміщення, d — коефіцієнт амортизатора, а V — швидкість пружини.
Це обчислює силу на основі зміщення пружини і гасить її залежно від швидкості. Коефіцієнти залежать від кроку симуляції та транспортного засобу, хороше правило для мене — почати з таких значень, де k більше за d в 10 разів. Досить просто, чи не так?
Далі, ми інтегруємо це в симуляцію, маючи основне фізичне тіло транспортного засобу і запускаючи промінь або форму вниз від початкової точки, де підвіска повинна бути прикріплена до кузова автомобіля, з максимальною довжиною підвіски (довжина спокою). У разі використання променевого трасування, зазвичай потрібно додати радіус колеса до цієї довжини. Залежно від того, яку інформацію про зіткнення видасть ваша фізична система, ви обчислюєте нову довжину (поточну довжину) підвіски. Якщо зіткнення не відбулося, можна тимчасово встановити поточну довжину рівною довжині спокою. Після цього обчислюєте зміщення і отримуєте силу підвіски за допомогою наведеної вище формули. Цю силу додаєте до точки фізичного тіла транспортного засобу, де підвіска повинна бути прикріплена.
Зробіть це 4 рази для чотириколісного транспортного засобу, і ви отримаєте своєрідну «глайдерну дошку», що піднімається над землею і реагує на падіння реалістичним способом.
Якщо ви хочете бачити рух коліс відповідно до цього, ви можете встановити їх позицію в напрямку підвіски * поточна довжина підвіски, залежно від того, як налаштована ваша ієрархія трансформацій.
Тепер перейдемо до основної теми цієї статті: моделі шини.
Модель шини
Моделі шин існують з єдиною метою — моделювання реалістичних явищ, таких як тертя гумової шини з землею. Оскільки гума є складним еластичним матеріалом, тертя не так просто обчислити.
Існує безліч моделей шин, кожна з яких має свої особливості та ефективність. У цій статті ми зосередимося на дуже відомій, економічній у обчисленнях і перевіреній часом серії моделей шин — Pacejka Magic Formula.
Magic Formula (скорочено MF) — це емпірична формула для опису сил тертя шини (Fx, Fy) як функції ковзання та опису моментів (Mx, My, Mz) навколо вертикальної осі шини. Спочатку розроблена завдяки роботі Ганса Б. Пачейки і профінансована Volvo та Audi VAG, він розробив серію формул, що описують вихідні сили тертя гуми під навантаженням та ковзанням. Це емпірична модель, що означає, що коефіцієнти, які використовуються як вхідні параметри, отримуються за допомогою підгонки кривих. Це процес отримання вихідних даних із реальних експериментів, а потім визначення констант для підгонки цих даних за допомогою MF. Оскільки таке повне дані про шини важко отримати, вони зазвичай належать корпораціям і рідко діляться.
MF досить інтуїтивно зрозуміла для використання, приймаючи вхідні параметри для кількості ковзання по боковому (кутовому) і поздовжньому (відношенню) ковзанню. Базова MF для сили тертя виглядає так:
де F — вихідна сила тертя в Н, {D,C,B,E} — константи, отримані з додаткових параметрів, а x — кількість ковзання.
Приклад C++ реалізації виглядає так:
float MF52(const MFTireIntermediate& intermediates, float slip)
{
slip += intermediates.H;
return intermediates.D * sinf(intermediates.C * atanf(intermediates.B * slip - intermediates.E * (intermediates.B * slip - atanf(intermediates.B * slip)))) + intermediates.V;
}
Коефіцієнти D (пік-фактор), C (фактор форми), B (фактор жорсткості) і E (фактор кривизни) обчислюються з додаткового набору констант, отриманих експериментальними даними, а обчислення з ними залежать від моделі шини, яку ви використовуєте. Більше про це в підрозділах моделей.
Існує також момент вирівнювання MF, але зазвичай його опускають, оскільки він не має відношення до вихідних сил шини. Момент вирівнювання — це момент, який шина отримує навколо вертикальної осі через бажання самовирівнятися. Однак я розповім про це в підрозділі MFTire 5.2.
Будь ласка, налаштуйте правильну локальну систему координат SAE, щоб терміни, такі як Fy і Fx, не були для вас заплутаними.
У цьому випадку шина зазнає поздовжнього (Fx) і бічного (Fy) тертя, що дає комбіновану силу тертя (Fcomb), вирівнювальний момент (Mz), а також нормальну силу / навантаження (Fz).
Тепер ми розглянемо формули для кількості ковзання, необхідної для MF, оскільки MF є функцією ковзання.
Є багато формул ковзання в Інтернеті, оскільки не всі з них налаштовані для динамічних сценаріїв, таких як ігри.
Для поздовжнього ковзання ми можемо обчислити коефіцієнт ковзання k таким чином:
slip_ratio = (tire.radius * angular_velocity - v_x) / fabs(v_x);
де angularvelocity — це кутова швидкість колеса в рад/с, vx — це швидкість в м/с, а tire.radius — це радіус шини в метрах.
vx_ — це швидкість шини, спроецьована на її поздовжню вісь. Ми можемо отримати vx_ легко, помноживши точкову швидкість контактної плями шини на поздовжню вісь шини. Зверніть увагу, що ми використовуємо fabs в знаменнику для підтримки змін знаків, оскільки ми хочемо, щоб ковзання могло бути від’ємним (уповільнення/гальмування).
Оскільки кутова швидкість, помножена на радіус, дає нам тангенційну (або лінійну) швидкість колеса, то k дає нам співвідношення швидкості ковзання (чисельник) до реальної швидкості дороги під контактною плямою (знаменник), що й називається коефіцієнт ковзання.
Для бічного ковзання ми можемо обчислити кут ковзання a так:
slip_angle = -atan2f(lateral_velocity, fabs(wheel.longitudinal_velocity));
де обидві швидкості виміряються в м/с, а slipangle в _рад. lateral_velocity — це швидкість контактної плями, спроецьована на бічну вісь шини, аналогічно до поздовжньої швидкості. Зверніть увагу на використання atan2f, оскільки ми хочемо отримати кут в правильному квадранті. Також зверніть увагу на негативний знак, оскільки це працює в моїй лівосторонній системі координат. І нарешті, ми використовуємо fabs, щоб уникнути проблем, коли поздовжня швидкість змінює знак. Бічна швидкість має бути головним фактором змін знаку.
Тепер, коли ми маємо необхідні кількості ковзання для MF, можемо продовжити говорити про дві різні моделі шин MF.
MF94
Спочатку я знайшов хороший ресурс MF 1994 року в пості від розробника, що займається симуляцією транспортних засобів для Unity. Це хороший і повний ресурс, де Еді описує свої знахідки щодо MF і параметрів, які потрібні, а також входи і виходи. Спосіб подачі інформації дозволяє швидко запустити щось у вашому проєкті. Він показує стандартні мінімальні та максимальні значення, стандартні форми формули, обчислення для проміжних факторів {D, C, B, E} і обчислення кількості ковзання. Якщо ви хочете щось, що є достатньо реалістичним і відносно швидким для впровадження, я раджу вам ознайомитись з його блогом.
Для мого проєкту я довго користувався цією моделлю, поки мені не знадобилася модель, яка могла б робити більше і не суперечила б SAEконвенціям. Ви можете помітити, що вхідні одиниці для моделі 1994 року описані у відсотках, градусах, а навантаження в кН, що не є стандартною практикою в роботах SAE. Це є проблемою тільки в тому випадку, якщо ви хочете використовувати інші матеріали, описані в цих роботах, або якщо ви не хочете постійно виконувати перетворення одиниць. Я просто знав про існування кращих моделей шин, тому це також відштовхнуло мене від цієї моделі.
MFTire 5.2
Розроблена TNO Automotive, ця модель є наступником MF, розробленої в 1994 році та наступних версій. Вона прагне бути відносно швидкою в обчисленнях і всеохоплюючою, що означає, що вона може добре працювати і ефективно використовуватись у широкому спектрі сценаріїв, якщо не у всіх. Існують різні рівні складності в моделі, залежно від того, скільки реалістичності вам потрібно.
Якщо ви ще тут, ймовірно, ви хочете дізнатися більше про спосіб отримання коефіцієнтів, необхідних для використання MF в цій моделі. Точніше, D, C, B та E. Що добре, то це те, що версії MF для бічної та поздовжньої сили спрощуються до кількох констант.
Отже, ми можемо створити структуру MFTireIntermediate, яка міститиме ці параметри:
struct MFTireIntermediate
{
//форма фактору
float C;
//пікове значення
float D;
//фактор пікового значення
float mu;
//фактор кривизни
float E;
//жорсткість ковзання (BCD), або жорсткість під час повороту
float K;
//фактор жорсткості
float B;
//горизонтальний зсув
float H;
//вертикальний зсув
float V;
};
Точний спосіб обчислення цих значень відрізняється для кожної версії. Як згадувалося раніше, ці параметри отримуються з інших констант. Для поздовжнього ковзання ми маємо всього 15 параметрів:
struct MFTireLongitudinal
{
//форма фактору
float Cx1;
//поздовжнє тертя при номінальному Fz
float Dx1;
//варіація тертя в залежності від навантаження
float Dx2;
//варіація тертя залежно від нахилу
float Dx3;
//поздовжня кривизна при номінальному Fz
float Ex1;
//варіація кривизни в залежності від навантаження
float Ex2;
//варіація кривизни в залежності від навантаження в квадраті
float Ex3;
//фактор кривизни під час руху
float Ex4;
//поздовжня жорсткість ковзання при номінальному fz
float Kx1;
//варіація жорсткості ковзання в залежності від навантаження
float Kx2;
//експонента у жорсткості ковзання з навантаженням
float Kx3;
//горизонтальний зсув при номінальному fz
float Hx1;
//варіація зсуву в залежності від навантаження
float Hx2;
//вертикальний зсув при fznom
float Vx1;
//варіація зсуву в залежності від навантаження
float Vx2;
};
Для бічних параметрів ми маємо загалом 18 параметрів:
struct MFTireLateral
{
//форма фактору
float Cy1;
//бічне тертя при номінальному Fz
float Dy1;
//варіація тертя в залежності від навантаження
float Dy2;
//варіація тертя залежно від нахилу в квадраті
float Dy3;
//бічна кривизна при номінальному Fz
float Ey1;
//варіація кривизни в залежності від навантаження
float Ey2;
//нулевий порядок залежності кривизни від нахилу
float Ey3;
//варіація кривизни в залежності від нахилу
float Ey4;
//максимальне значення жорсткості fy при fz nom
float Ky1;
//навантаження, при якому kfy досягає максимального значення
float Ky2;
//варіація kfy/fznom залежно від нахилу
float Ky3;
//горизонтальний зсув при номінальному fz
float Hy1;
//варіація зсуву в залежності від навантаження
float Hy2;
//варіація зсуву залежно від нахилу
float Hy3;
//вертикальний зсув при fznom
float Vy1;
//варіація зсуву в залежності від навантаження
float Vy2;
//варіація зсуву залежно від нахилу
float Vy3;
//варіація зсуву залежно від нахилу та навантаження
float Vy4;
};
Це константи, отримані з даних, що були отримані за допомогою підгонки кривих з реальних експериментів. Мабуть, найскладніша частина цього процесу — це знайти повні та сумісні набори даних для MFTire 5.2.
Не хвилюйся, я надам тобі кілька повних ресурсів:
Коефіцієнти PAC2002 з OpenTire
Ці ресурси містять усі коефіцієнти, необхідні для MF5.2, якщо не більше (Sample.tir навіть має коефіцієнти для MF6.2).
Тепер перейдемо до розрахунків поздовжніх проміжних параметрів за допомогою цих констант:
Я зекономлю тебе від написання коду на C++:
MFTireIntermediate GetMFTireIntermediate(const MFTireLongitudinal& params, const MFTireScaleParams& scaling, MFTireState state)
{
MFTireIntermediate long_intermediates;
//Yx = y * mu y
state.camber *= scaling.l_camber;
//Shx
long_intermediates.H = (params.Hx1 + params.Hx2 * state.normalized_load_increment) * scaling.l_horizontal_shift;
//Kx = k + Shx
state.slip_ratio += long_intermediates.H;
long_intermediates.C = params.Cx1*scaling.l_shape_factor;
long_intermediates.mu = (params.Dx1 + params.Dx2*state.normalized_load_increment) * (1.f - params.Dx3 * (state.camber*state.camber)) *
scaling.l_peak_friction_coefficient;
long_intermediates.D = long_intermediates.mu * state.fz;
long_intermediates.E = (params.Ex1 + params.Ex2 * state.normalized_load_increment + params.Ex3*(state.normalized_load_increment*state.normalized_load_increment)) *
(1.f - params.Ex4*sign(state.slip_ratio)) * scaling.l_curvature_factor;
long_intermediates.K = state.fz * (params.Kx1 + params.Kx2 * state.normalized_load_increment) * glm::exp(params.Kx3*state.normalized_load_increment) *
scaling.l_slip_stiffness;
long_intermediates.B = long_intermediates.K / (long_intermediates.C * long_intermediates.D);
long_intermediates.V = state.fz * (params.Vx1 + params.Vx2*state.normalized_load_increment) * scaling.l_vertical_shift * scaling.l_peak_friction_coefficient;
return long_intermediates;
}
Для бічних проміжних параметрів:
Знову ж таки, зекономлю тобі час:
MFTireIntermediate GetMFTireIntermediate(const MFTireLateral& params, const MFTireScaleParams& scaling, MFTireState state)
{
MFTireIntermediate lat_intermediates;
state.camber *= scaling.l_camber;
//Shy
lat_intermediates.H = (params.Hy1 + params.Hy2*state.normalized_load_increment) * scaling.l_horizontal_shift + params.Hy3 * state.camber;
//alphay = alpha + Shy
state.slip_angle += lat_intermediates.H;
lat_intermediates.C = params.Cy1 * scaling.l_shape_factor;
lat_intermediates.mu = (params.Dy1 + params.Dy2 * state.normalized_load_increment) * (1.f - params.Dy3 * (state.camber*state.camber)) * scaling.l_peak_friction_coefficient;
lat_intermediates.D = lat_intermediates.mu * state.fz;
lat_intermediates.E = (params.Ey1 + params.Ey2 * state.normalized_load_increment) * (1.f - (params.Ey3 + params.Ey4 * state.camber) * sign(state.slip_angle)) *
scaling.l_curvature_factor;
lat_intermediates.K = params.Ky1 * nominal_load * sinf(2.f*atanf(state.fz / (params.Ky2 * nominal_load * scaling.l_nominal_load) )) *
(1.f - params.Ky3 * fabs(state.camber)) * scaling.l_nominal_load * scaling.l_slip_stiffness;
lat_intermediates.K *= -1.f;
lat_intermediates.B = lat_intermediates.K / (lat_intermediates.C * lat_intermediates.D);
lat_intermediates.V = state.fz * ((params.Vy1 + params.Vy2 * state.normalized_load_increment) * scaling.l_vertical_shift + (params.Vy3 + params.Vy4 * state.normalized_load_increment)
* state.camber) * scaling.l_peak_friction_coefficient;
return lat_intermediates;
}
Можна помітити, що входи MFTireScaleParams і MFTireState використовуються разом з аргументами функції. Перший з них є просто контейнером для коефіцієнтів масштабування, а другий — поточним станом шини.
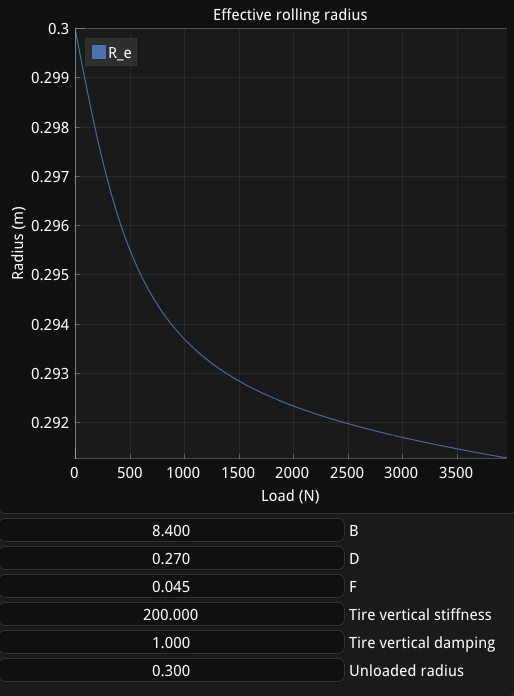
Папір апроксимує для легкового автомобіля: B = 8.4, D = 0.27 та F = 0.045.
Номінальний дефлекцій шини (тиску) обчислюється за формулою:
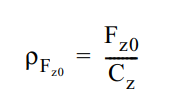
Де Cz — вертикальна жорсткість шини в Н/мм (я використовував діапазон 100–250).
Безрозмірний радіальний дефлексія шини обчислюється за формулою:
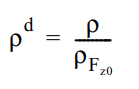
Де Pfz0 — номінальний дефлексія шини, а p — радіальний дефлексія шини.
Радіальний дефлексія шини обчислюється так:
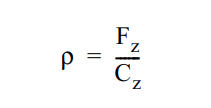
Де Cz — вертикальна жорсткість (Н/мм), а Fz — навантаження (Н).
Щоб зробити ефективний радіус більш стабільним і не викликати зворотну зв'язок, у статті використовується кращий метод обчислення для **Fz**:
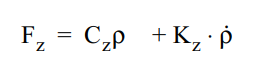
Де Cz — вертикальна жорсткість шини (Н/мм), p — радіальний дефлексія шини, Kz — вертикальний коефіцієнт демпфування, а p_deriv — швидкість зміни дефлекції.
Як ви можете помітити, введено термін демпфування. Також, _Cz * p_ спрощується до просто вхідного значення _Fz_ від нашої підвіски, оскільки дефлекція _p_ це _Fz_/_Cz_.
Зрештою, побудова графіка ефективного радіусу кочення _Re_ показує, що радіус різко зменшується, а потім знижується з збільшенням навантаження:
Як завжди, я заощаджую ваш час, надаючи приклад реалізації:
float GetEffectiveRollingRadius(const MFTireRubberParams& tire_params, float fz)
{
//TODO: optimize
//номінальний дефлексія шини (мм)
float nominaltiredeflection = nominalload / tireparams.C_z;
//поточний дефлексія шини (мм)
float tiredeflection = fz / tireparams.C_z;
//безрозмірний радіальний дефлексія шини
float tiredeflectiond = tiredeflection / nominaltire_deflection;
//магічна формула для ефективного радіусу кочення під навантаженням, MFTyre (4)
return tireparams.R0 - (nominaltiredeflection0.001f) * (tire_params.Datanf(tireparams.B*tiredeflectiond) + tireparams.F*tiredeflectiond);
}
```
Зверніть увагу, що я змушений був ввести перетворення одиниць з мм на м для номінальної дефлекції шини, щоб вона мала сенс. У статті це не є очевидним, і я не впевнений, чи є це помилкою чи ні. В будь-якому випадку, результати збігаються з результатами, отриманими в статті.
Окрім базового MF, який є тим самим, що згадано на початку глави, MFTire містить MF для крутного моменту вирівнювання. Моменти вирівнювання (M) — це моменти, що змушують шину самовирівнюватись, коли її справжній напрямок відрізняється від поточного поздовжнього напрямку, фактично коли виникає позитивний кут ковзання |a|.
Коли ви передаєте вхід на рульове колесо, ви відчуваєте силу зворотного зв'язку (або, точніше, крутний момент) від цього моменту вирівнювання навколо вертикальної осі шини, що передається через рульовий механізм до рульового колеса.
Формула для моменту вирівнювання задана такою:
Де Mz — момент вирівнювання, t — пневматична слідність, Fy — бічна сила та Mzr — залишковий момент.
Пневматична слідність t задається косинусною версією MF:
Де D,C,B,E — константи, отримані з проміжних розрахунків, a — кут ковзання (рад), at — горизонтально відкоригований кут ковзання._
Залишковий момент Mzr задається такою формулою:
Де D і B — проміжні константи, отримані подальшими обчисленнями, a — кут ковзання (рад), а ar — горизонтально відкоригований кут ковзання.
Я не буду детально зупинятися на моментах вирівнювання, оскільки вони не є основною темою цієї статті, і вам вони навряд чи знадобляться, якщо ви не хочете реалістичного зворотного зв'язку сил і фізично симульованої вертикальної осі.
Інші явища, що можна моделювати
Модель може симулювати й інші цікаві явища, що виникають при русі гумового колеса та його обертанні. Більшу точність моделювання можна досягти за допомогою цих явищ.
- Опір коченню гуми
Коли шина обертається по поверхні, гума фактично трохи стискається перед центром контакту, а потім розтягується, коли на певну відстань пройдено відносно контакту.
Це призводить до втрати енергії, що описується моментом опору коченню (My) у вигляді MF:
Де R0 — радіус без навантаження (м), Fz — навантаження (Н), qsy1,2,3,4 — константи, отримані з набору даних, Vx — поздовжня швидкість (м/с), а Vref — номінальна поздовжня швидкість, при якій шину тестували.
Vref зазвичай знаходиться разом з набором даних.
- Перехідна реакція
Гумова шина не реагує на зміни миттєво, вона дещо запізнюється при змінах стану ковзання. Це пов'язано з тим, що контактна пляма шини прилипає до поверхні через еластичність гуми, яка не дотримується відразу нових змін обертання колеса.
Джерело: TNO MFTire презентація
MFTire здатен непогано моделювати перехідні явища, зокрема моделі жорсткості каркаса та перехідні сили контактної плями. Проте на момент написання я ще не реалізував і не дослідив це питання досить глибоко, щоб впевнено про це говорити. Коли я це зроблю, оновлю статтю відповідно.
- Гіроскопічний момент
Гіроскопічний момент — це цікавий ефект, що виникає, коли колесо починає обертатися досить швидко і стає гіроскопом, що чинить опір руху вздовж вертикальної осі, що відчувається в інших моментах вирівнювання. Формулу для цього моменту можна розрахувати за допомогою:
Де cgyr розраховується за допомогою коефіцієнта масштабування та константи з набору даних, mbelt — маса ременя, Vrl — відносна швидкість.
Cgyr розраховується за такою формулою:
Де qTzl — гіроскопічна константа моменту, а lambda — коефіцієнт масштабування.
- Функціональність обгортання шини
Оскільки шина виготовлена з гуми, вона може деформуватися навколо дуже малих перешкод, тобто обгортати їх. Коли шина є жорсткою, така поведінка неможлива.
Отже, MFTire має здатність моделювати модель обгортальної шини:
Я не зовсім впевнений, чи потрібно все ж таки враховувати перехідні явища, якщо ви реалізуєте поведінку обгортання, оскільки виглядає, що ви вже подовжуєте час відгуку! Джерело: TNO MFTire презентація
Для моделювання цієї складної поведінки MFTire надає нам модель подвійної камери обгортання:
Джерело: TNO MFTire презентація
Очевидно, це більше стосується реального моделювання шин, але все одно дуже цікаво бачити, як така модель шини поступово стає більш складною. Однак я не буду сильно заглиблюватися в це, оскільки не вважаю це достатньо корисним для негайної реалізації. Лише коли необхідна висока точність моделювання на цьому рівні, слід розглянути реалізацію такої моделі.
Загальні проблеми та рішення з MF
Магічні формули чудові, але вони не позбавлені недоліків. Існують деякі критичні проблеми, які потрібно вирішити, використовуючи їх. Я розгляну їх і поясню, як я їх вирішив. Більшість статей, згаданих нижче, знаходяться за платним доступом, але я дам DOI, і розумна людина зможе знайти способи безкоштовного доступу до статей через певні сайти.
- Сингулярність при нульовій швидкості: Вхідні параметри для магічних формул містять поздовжню швидкість шини в знаменнику. Тому, коли швидкість автомобіля наближається до нуля, вихідні значення стають чисельно нестабільними і наближаються до сингулярності. На щастя, це поширена проблема в симуляціях автомобілів, і кілька статей пропонують рішення для її усунення.
Деякі статті, що пропонують рішення (в порядку зростання дати публікації):
LSR (Lagged slip ratio, Бенард і Кловер) пропонує вирішення цієї проблеми шляхом інтегрування коефіцієнта ковзання в диференціальному рівнянні, а не обчислення його безпосередньо. DOI: 10.4271/950311
ASR (Advanced slip ratio, Юнг та ін.) вирішує цю проблему, аналізуючи нестабільність і забезпечуючи збіжність до чисельно стабільного результату. DOI: 10.1177/0954407018759738
ALSR (Advanced lagged slip ratio, Юнг та ін.) поєднує затриманий і просунутий коефіцієнт ковзання для забезпечення стабільності при низьких і високих швидкостях в симуляції автомобіля. DOI: 10.1007/s12206–020–0110-y
Після реалізації одного або кількох з цих рішень, ви можете протестувати їх і побачити їх ефект. Ці рішення є важливими для досягнення стабільності при їзді на низьких швидкостях для реалістичної поведінки.
- Бічне тертя не масштабується зі зміною бічної швидкості
Як видно з розрахунків коефіцієнта ковзання, для коефіцієнта ковзання ми обчислюємо поздовжню швидкість ковзання (різниця лінійних швидкостей шини та напрямку руху) і використовуємо її для порівняння з лише поздовжньою швидкістю. Це дає нам коефіцієнт, що вимірює, як швидко шина обертається відносно землі. Таким чином, коефіцієнт ковзання вже враховує швидкість ковзання для поздовжньої сили. Для кута ковзання ми все ще використовуємо компонент швидкості Vsy, що є бічною швидкістю ковзання контактної плями. Але ми ділимо її на поздовжню швидкість, щоб отримати вхід для арктангенса, який обчислює кут між справжнім напрямком шини та її напрямком руху. Ми не використовуємо це для отримання коефіцієнта, що вимірює, як швидко змінюється бічна швидкість ковзання.
Цей кут ковзання не враховує бічну швидкість, яку відчуває шина. Крім того, при низьких швидкостях абсолютний кут ковзання буде близьким до кута +-90 градусів через низьку поздовжню швидкість. Це генерує значні бічні сили, постійно коливаючи автомобіль в бічному напрямку шини на стоянці, хоча це й не потрібно.
Ми можемо краще використовувати поздовжню силу для утримання автомобіля на місці, оскільки більша бічна сила зменшує поздовжню силу на деяку величину.
Як я вирішив це: використовую лише бічну силу, коли це необхідно:
wheel.lateral_slip_factor = fmin(fabs(lateral_velocity*3.f) + fabs(wheel.steering_angle)/vehicle.max_steering_angle, 1.f);
Ефективно я використовую коефіцієнт масштабування для зміни fx. Коефіцієнт масштабування залежить від бічної швидкості, помноженої на 3, оскільки це здається достатнім для збільшення бажаної чутливості, не використовуючи всю здатність бічної сили на місці. Це також працює для мого розміру одиниць. Додатково я додаю залежність для кута повороту, оскільки ми хочемо миттєво помічати новий напрямок шини, який починає діяти, а не чекати, поки бічна швидкість стане достатньо великою.
- Одна з формул (бічної чи поздовжньої) є дійсною, коли інша не є.
Вихід бічної MF Fx(a) є правильним лише тоді, коли MF для поздовжньої сили Fy(k) = 0, і навпаки. Тому нам потрібно знайти спосіб поєднати ці дві сили в одну комбіновану силу ковзання, оскільки шина може видавати лише певну кількість сили тертя. Ви можете думати про це як про нормалізацію сил у вектор сили. Оскільки величина бічної та поздовжньої сили прямо залежить від навантаження, вони є дійсними тільки для всього цього діапазону і коли протилежна сила = 0. Інакше шина може видавати до +-8000 Н при піковому ковзанні при навантаженні 4000 Н.
Існує кілька методів для отримання комбінованого ковзання з магічних формул, і я розгляну 4 з них.
Метод 1: Я бачив реалізації, де поздовжня сила (Fx) переважала над бічною силою (Fy), і бічна сила зменшувалася, поки величина вектора сили знову не досягала максимуму. Це просте рішення є швидким способом стабільно протестувати інші важливі динаміки стабільності моделі, але воно не є дуже гнучким у сценаріях, коли шина відчуває значний бічний і поздовжній ковзання. Оскільки Fy зменшується на користь Fx, автомобіль або сильно недосконало входить в повороти, або надмірно перебирає, залежно від конфігурації трансмісії.
Метод 2: У "Physics of Racing" Брайан Бекман, чудовому ресурсі для фізичних динамік автомобілів, з комбінованим ковзанням він спочатку зазначає:
“Є багато способів об’єднати їх. Це не той випадок, коли є один правильний відповідь. Натомість, за відсутності жорсткої теорії або експериментальних даних, ми маємо свободу бути креативними, з неминучим ризиком помилки. Ми обираємо метод, який задовольняє деякі прості, інтуїтивні фізичні вимоги.”
Це гарний спосіб сказати, що наступне — це не абсолютно “правильний” підхід і не повинно сприйматися як абсолютна істина, але це логічний підхід до проблеми.
Як видно вище, Брайан використовує підхід масштабування входів через коефіцієнт пікової сили зчеплення. Він спочатку обчислює максимуми Fx і Fy, що вже є проблемним, оскільки це вимагає похідної магічної формули при певному навантаженні, і оскільки в новій моделі шини є фактори, що залежать від навантаження, обчислення похідної на кожному такті є великим завданням. Потім він використовує ці максимуми для отримання відношення поточної сили до максимального, отримуючи безрозмірне співвідношення коефіцієнтів ковзання s і a. Він потім нормалізує їх до максимального p, який використовує для масштабування звичайних Fx і Fy відповідно до s та a. Це, по суті, дає нам сили в межах кола зчеплення навколо максимального ковзання.
Метод 3: MFTire 5.2 має інший набір емпіричних функцій з магічної формули з кривими коефіцієнтами, що зменшують чисті Fx та Fy відповідно.
Ми можемо краще використовувати поздовжню силу для того, щоб утримати транспортний засіб на місці, оскільки більша поперечна сила зменшує поздовжню силу на деяку величину.
Як я вирішив цю задачу, використовуючи лише поперечну силу, коли це необхідно:
wheel.lateral_slip_factor = fmin(fabs(lateral_velocity*3.f) + fabs(wheel.steering_angle)/vehicle.max_steering_angle, 1.f);
Ефективно я використовую коефіцієнт масштабування для масштабування fx. Коефіцієнт масштабування залежить від поперечної швидкості, помноженої на 3, оскільки це здається достатнім для збільшення бажаної чутливості, при цьому не використовує всю можливість поперечної сили під час стояння. Це також працює для мого розміру одиниць. Додаю також залежність від кута повороту, оскільки ми хочемо миттєво помітити зміну напрямку колеса, замість того, щоб чекати, поки поперечна швидкість стане достатньо великою.
3. Лише поперечна або поздовжня формула є дійсною, коли інша не є.
Поперечна MF Fx(a) є дійсною лише тоді, коли MF для поздовжньої сили Fy(k) = 0, і навпаки. Тому нам потрібно знайти спосіб поєднати дві сили в комбіновану силу ковзання, оскільки шина може вивести лише певну кількість сили тертя. Ви можете уявити це як нормалізацію сил у силовий вектор. Оскільки величина поперечних і поздовжніх сил прямо залежить від навантаження, вони є дійсними лише для всього цього діапазону та коли протилежна сила = 0. Інакше шина може вивести ±8000 Н при піковому ковзанні на навантаженні 4000 Н.
Існує кілька методів отримання комбінованого ковзання з магічних формул, і я детально опишу 4 з них.
Техніка 1: Я бачив реалізації, де поздовжня сила (Fx) має перевагу над поперечною силою (Fy), і поперечна сила зменшується, поки величина силового вектора знову не стане максимальною. Це просте рішення є швидким способом стабільно тестувати інші критичні динаміки стійкості моделі, але не є досить прощаючим у сценаріях, де шина переживає значне поперечне і поздовжнє ковзання. Оскільки Fy зменшується на користь Fx, автомобіль або сильно недоводиться, або перевертається, в залежності від конфігурації приводу.
Техніка 2: У книзі «Фізика гонок» Брайана Бекмана, чудовому ресурсі з фізичних динамік транспортних засобів, щодо комбінованого ковзання він спочатку зауважує:
“Є багато способів, як ми можемо поєднати їх. Це не та ситуація, де є один правильний відповідь. Замість цього, за відсутності твердої теорії або експериментальних даних, у нас є свобода бути творчими, з неминучим ризиком бути неправими. Ми обираємо метод, який задовольняє деякі прості, інтуїтивні фізичні вимоги.”
Це гарний спосіб сказати, що наступне не є абсолютним “правильним” підходом і що це не слід сприймати як істину, а радше як логічний підхід до проблеми.
Як видно вище, Брайан обирає підхід масштабування вхідних даних за допомогою коефіцієнта максимального кола зчеплення. Спочатку він обчислює максимуми Fx і Fy, що вже є проблематичним, оскільки це вимагає похідної магічної формули при певному навантаженні, а оскільки в новішій моделі шини існують фактори, що залежать від навантаження, обчислення похідної на кожному кроці є великою задачею. Потім він використовує ці максимуми для отримання співвідношення поточного значення до максимальних, отримуючи безрозмірні співвідношення ковзання s і a. Потім він нормалізує їх до максимального p, яке він потім використовує для масштабування нормальних Fx і Fy відповідно до s і a. Це, по суті, дає нам сили фрикційного кола навколо максимального ковзання.
Техніка 3: MFTire 5.2 має ще один набір емпіричних вагових функцій магічної формули з криваво підігнаними константами, що зменшують чисті Fx і Fy відповідно.
Ці вагові функції є магічними формулами (MF):
Де Fx0 — чисте поздовжнє тертя, Gxa — вагова функція
Вагова функція Gxa обчислюється як:
Де as — горизонтально зсунутий кут ковзання, Cxa, Bxa, Exa, Shxa — константи, обчислені за допомогою подальших констант набору даних
Горизонтально зсунутий кут ковзання:
Отримання Cxa, Bxa, Exa, і Shxa виглядає наступним чином:
Де rBx1, rBx2, rCx1, rEx1, rEx2, rHx1 — це всі константи набору даних, dfz — нормалізоване збільшення навантаження, k — коефіцієнт ковзання, а lambda — коефіцієнт масштабування. Зверніть увагу на Dxa, у статті пояснюється похідне для вагової функції.
Обчислення комбінованого поперечного ковзання є подібним, я швидко вставлю їх для вас:
З ваговою функцією Gyk:
І обчислення коефіцієнта:
з новим з’являючимся y як кут нахилу (camber angle) (рад).
Я ще не реалізував цю форму комбінованого ковзання, тому поки не можу надати код для цього методу.
Техніка 4: Існує десятки інших технік для комбінування ковзаючих сил, але одна цікава, яку я знайшов, є на вебсайті ADAMs/Tire, стандартного програмного забезпечення для симуляції транспортних засобів в індустрії. Вони мають пояснення моделей Pacejka 89 і 94, з власним способом комбінування ковзаючих сил. Цитата з їхнього вебсайту:
"Обчислення комбінованого ковзання для моделей шин Pacejka '89 та '94 є ідентичним."
Зверніть увагу, що метод, використаний тут, не є частиною магічної формули (Magic Formula), розробленої професором Пейчека, а є власною розробкою MSC.
Де обчислення beta:
де k — коефіцієнт ковзання, a — кут ковзання (рад).
Для цього у мене є повна реалізація на C++ для вас:
glm::vec2 GetCombinedSlipMSC(float fx, float fy, float fz, float slip_ratio, float slip_angle, const MFTireIntermediate& long_factors, const MFTireIntermediate& lat_factors)
{
//Власна реалізація MSC, ADAMs/tire
//https://nexus.hexagon.com/documentationcenter/en-US/bundle/adams_2022.1/page/adams_help/Adams_Car_Package/tire/tire_models_pacgeneric/TOC.Combined.Slip.of.Pacejka.xhtml
float a_slip_ratio = slip_ratio + long_factors.H;
float a_slip_angle = slip_angle + lat_factors.H;
float SAG = sinf(a_slip_angle);
float SAG_sqr = SAG * SAG;
float a_slip_ratio_sqr = a_slip_ratio * a_slip_ratio;
float beta = acosf(fabs(a_slip_ratio) / (sqrtf(a_slip_ratio_sqr + SAG_sqr) + FLT_EPSILON));
//Обчислення коефіцієнтів тертя
//актуальний поздовжній коефіцієнт
float mu_x_act = (fabs(fx - long_factors.V) / (fz + FLT_EPSILON)) + FLT_EPSILON;
//актуальний поперечний коефіцієнт
float mu_y_act = (fabs(fy - lat_factors.V) / (fz + FLT_EPSILON)) + FLT_EPSILON;
//максимальні коефіцієнти
float mu_x_max = (long_factors.D / (fz + FLT_EPSILON)) + FLT_EPSILON;
float mu_y_max = (lat_factors.D / (fz + FLT_EPSILON)) + FLT_EPSILON;
//тепер обчислюємо коефіцієнти тертя mu
float mu_x = 1.f / sqrtf((1.f / mu_x_act) * (1.f / mu_x_act) + (tanf(beta) / mu_y_max) * (tanf(beta) / mu_y_max));
float mu_y = tanf(beta) / sqrtf((1.f / mu_x_max) * (1.f / mu_x_max) + (tanf(beta) / mu_y_act) * (tanf(beta) / mu_y_act));
float fx_combined = (mu_x / mu_x_act) * (fx + long_factors.V);
float fy_combined = (mu_y / mu_y_act) * (fy + lat_factors.V);
return glm::vec2(fx_combined, fy_combined);
}
Як видно з вище, метод, який вони використовують, схожий на метод коефіцієнта масштабування, також використаний у техніці 2. Ми обчислюємо μ актуальний і μ максимальний для кожної частини сили, потім обчислюємо остаточний коефіцієнт тертя μ, щоб масштабувати з μ max для отримання скаляра від 0 до 1, а потім використовуємо це для зменшення чистої сили тертя Fx і Fy. Що цікаво в цьому методі — це відносно легка реалізація, яка враховує величини ковзання для отримання остаточних сил.
В кінцевому рахунку, ви тестуєте багато технік і дивитесь, яка з них найкраща для вашого типу гри.
Висновок
Я думаю, ми достатньо поговорили про моделі шин та їх специфіку, оскільки стаття вийшла досить довгою. Метою цієї статті є поділитися з вами знаннями, читачу, щоб ви могли заощадити час, який я витратив на пошук і дослідження цієї інформації. Якщо вийде частина II, ми поговоримо про симуляцію динаміки двигуна внутрішнього згоряння та симуляцію трансмісії.
Сподіваюся, вам сподобалося читати, і якщо у вас є питання чи ви помітили які-небудь невідповідності, обов'язково дайте мені знати.
Перекладено з: How to program realistic vehicle physics for realtime environments / games, Part I: simple suspension and realistic tire dynamics (C++)